
En la entrada anterior, les platiqué cómo se modela un motor de corriente directa . En esta entrada les mostraré como se puede realizar una simulación utilizando herramientas de código abierto; en este caso: el lenguaje de programación Python. Pero antes, un poco de teoría.
Integrales y derivadas numéricas
Si recuerdan sus clases de cálculo, seguramente recordaran que la integral es el “área bajo la curva” y la derivada: “la recta tangente a la curva” que los profesores repiten hasta casi hacernos vomitar. Pero, ¿cuál es el significado en la realidad, o la aplicación práctica de una integral o una derivada? En este caso, les presento una: resolver ecuaciones diferenciales de forma numérica. Esto no es importante solo por el hecho de que sea tedioso o aburrido resolver ecuaciones diferenciales de forma analítica y a mano como en sus exámenes de cálculo. Verán, la mayoría de las ecuaciones diferenciales que representan fenómenos físicos son demasiado complejas para resolver de forma analítica, y en muchos otros casos las soluciones ni siquiera existen. Entonces, podemos recurrir a las computadoras para resolver las ecuaciones diferenciales y poder estudiar la respuesta de los modelos bajo diferentes condiciones.
Podrían pensar que, si de por si ya es complicado resolver una integral o derivada en lápiz y papel, ha de ser aún más difícil resolverlas con una computadora. Están equivocados. Déjenme aburrirlos con un poco de teoría. Será breve. Lo prometo.
Es posible aproximar una integral de la siguiente forma:
$$\int_a^bf(x)\mathrm{d}x=\sum_{k=a}^b f(x)\Delta x$$
La sumatoria converge a la integral cuando $\lim\Delta x \to 0$, pero esto no nos interesa mucho ahorita: nos interesa la sumatoria. Entonces, vemos que podemos aproximar una integral con una sumatoria, siempre y cuando Δ sea lo suficientemente pequeño. De manera similar, podemos aproximar la derivada
$$\frac{\Delta f(x)}{\Delta x}\approx \frac{\mathrm{d}f(x)}{\mathrm{d}x},$$
si $\Delta x$ es suficientemente pequeño. Entonces todo esto comienza a tomar sentido. Las integrales se vuelven sumas, mientras que las derivadas se vuelven restas. !Esto sí es sencillo! Veamos cómo podemos usar estas aproximaciones para simular el motor de la entrada anterior:
$$ \frac{\Omega(s)}{V_{in}(s)}=\frac{K}{\tau s + 1},$$
donde $K$ es la ganancia de DC del sistema y $\tau$ es la constante de tiempo. Demos un paso atrás y transformaremos este modelo de una función de transferencia a una ecuación diferencial de primer orden:
$$ \tau\frac{\mathrm{d}\omega}{\mathrm{d}t}+\omega=Kv_{in}, $$
donde $\omega$ es la velocidad del motor y $v_{in}$ es el voltaje de entrada. El objetivo es encontrar la evolución de ω en el tiempo. Cambiemos la derivada por la aproximación que definimos anteriormente:
$$ \tau\frac{\Delta\omega}{\Delta t}+\omega=Kv_{in} ,$$
¿Y qué representa la fracción $\frac{\Delta\omega}{\Delta t}$ realmente? Sólo representa la magnitud del cambio de la velocidad del motor de un instante anterior al momento actual. Este es el significado en la realidad de una derivada: es la medida del cambio de una variable: posición, velocidad, voltaje, corriente, etc. Podemos usar las derivadas para obtener la medida del cambio de señales que nos interesan. Entonces, si esta fracción representa el cambio en la velocidad, podemos redefinir la ecuación de diferencias (ya no es ecuación diferencial, pues aproximamos la derivada con una resta y división):
$$ \frac{\omega_k-\omega_{k-1}}{\Delta t} \approx \frac{1}{\tau}(Kv_{in}-\omega_{k-1}), $$
donde $\omega_k$ es la velocidad en el instante actual, y $\omega_{k-1}$ en el instante anterior. ¿Qué variable es la que nos interesa? La velocidad el motor en el instante actual. Entonces, solo necesitamos resolver la ecuación algebraica y listo:
$$ \omega_k \approx \frac{\Delta t}{\tau}(Kv_{in}-\omega_{k-1})+\omega_{k+1}, $$
Esta es la ventaja de resolver una ecuación diferencial en una computadora: las integrales se transforman en sumas y las derivadas en restas. Una ecuación diferencial se vuelve una ecuación de diferencias.
Simulación del motor en Python
De nada nos sirve la ecuación si no podemos estudiar la respuesta. Podemos resolverla paso a paso y obtener la evolución del sistema; sin embargo, estarán de acuerdo que esto sería tedioso y aburrido. Por otro lado, las computadoras son perfectas para esto. Existen diversas herramientas de simulación y lenguajes de programación tanto libres como propietarios para simular sistemas. En esta ocasión usaremos Python por la sintaxis tan limpia que caracteriza a este lenguaje y además, es un lenguaje de programación de código abierto.
La simulación del motor es algo así:
# Importar modulo para graficar.
import matplotlib.pyplot as plt
K = 145.47 # Ganancia de DC del motor.
tau = 0.087 # Constante de tiempo,
ti = 0. # Tiempo inicial.
tf = 2. # Tiempo final.
dt = 0.01 # Tiempo de muestreo.
t = ti # Tiempo actual de simulacion.
Vin = 24 # Voltaje de entrada.
w = 0. # Velocidad inicial del motor.
W = [w] # Vector de soluciones.
T = [t] # Vector de tiempo.
ts = 1e-2 # Tiempo de muestreo.
# Integrar la ecuacion de diferencias
# por el tiempo especificado.
while t < tf:
# Esta es la ecuacion de diferencias.
w = (dt / tau) * (K * Vin - w) + w
t += ts # Siguiente muestra de tiempo.
# Agregar al vector de soluciones para graficar
# la velocidad contra el tiempo.
W.append(w / 1000.)
T.append(t)
# Graficar la velocidad contra el tiempo.
plt.plot(T, W)
# Adornar la grafica.
plt.title('Respuesta del motor')
plt.xlabel('Tiempo (s)')
plt.ylabel('Velocidad (RPM x 1000)')
plt.show()
La gráfica debería verse similar a esta:
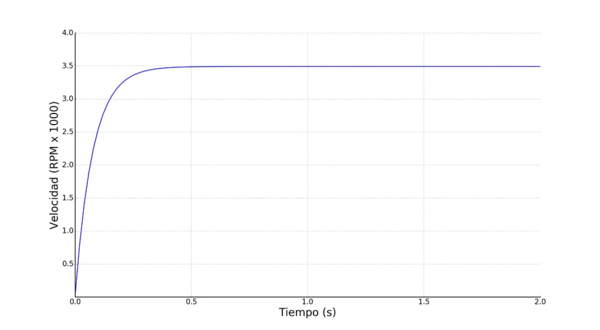 Figura 1.- Respuesta del motor de corriente directa a un escalón de voltaje.
Figura 1.- Respuesta del motor de corriente directa a un escalón de voltaje.
Simular sistemas dinámicos utilizando métodos numéricos permite evaluar el desempeño del sistema a variación de parámetros: sea del sistema mismo, condiciones de operación, diferentes paradigmas de control, etc. Por ejemplo, supongamos que queremos estudiar el impacto de la variación de los parámetros τ,K. Si tienen conocimiento en teoría de ecuaciones diferenciales, les será obvio el impacto que tienen estos parámetros en la respuesta del motor. Pero tengamos en cuenta que estamos hablando de un sistema lineal de primer orden; no es tan sencillo deducirlo para modelos de sistemas dinámicos más complejos.
Supongamos que el modelo es más complejo y queremos estudiar el impacto de estos parámetros usando Python. ¿Cómo sería?
import matplotlib.pyplot as plt
# Vectores de variacion de parametros
_K = [145.47 * (i / 2.) for i in range(2, 7)]
_tau = [0.087 * (i / 2.) for i in range(2, 7)]
ti = 0. # Tiempo inicial.
tf = 1.5 # Tiempo final.
ts = 0.02 # Tiempo de muestreo.
t = ti # Tiempo actual de simulacion.
Vin = 24 # Voltaje de entrada.
x = 0. # Velocidad inicial del motor.
_X = [[x] for _ in _K] # Vector de soluciones
_T = [[t] for _ in _K] # Vector de tiempo
# Leyendas
leg = []
for K, tau, X, T in zip(_K, _tau, _X, _T):
x, t = X[0], T[0]
# Asignar leyenda para distinguir grafico.
leg.append('K={0}, tau={1}'.format(K, tau))
while t < tf:
dx = (K * Vin - x) / tau
x += dx * ts
t += ts # Siguiente muestra de tiempo.
X.append(x / 1000)
T.append(t)
plt.plot(T, X, linewidth = 2.)
plt.title('Impacto de la Variacion de Parametros del Motor')
plt.xlabel('Tiempo (s)')
plt.ylabel('Velocidad (RPM x 1000)')
plt.xlim([ti, tf])
plt.grid()
plt.legend(leg, loc='best')
plt.show()
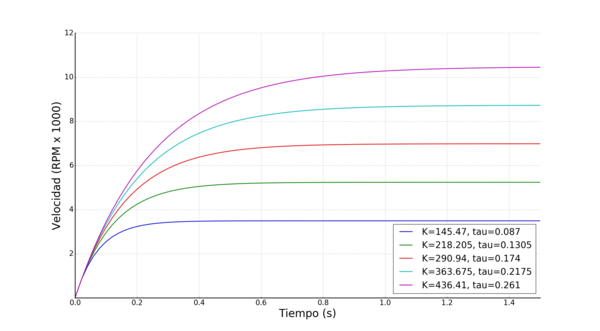 Figura 2.- Respuesta del motor con diferentes parámetros a un escalón de voltaje.
Figura 2.- Respuesta del motor con diferentes parámetros a un escalón de voltaje.
Se puede apreciar en la Figura 2 que el impacto de la constante de tiempo $\tau$ es aumentar o disminuir la respuesta del motor, mientras que la ganancia $K$ determina la magnitud que alcanza la velocidad: tal como lo esperábamos.
Entonces, podemos concluir que fácilmente podemos desarrollar simulaciones para estudiar la respuesta de sistemas dinámicos bajo condiciones de operación que nos interesen.
Integrador ODE-1
Podemos establecer un algoritmo un poco más sencillo de recordar que nos permitirá desarrollar las simulaciones aún con más facilidad: el método de integración “ODE-1” o método de Euler. Va algo así: redefinamos, por sencillez, la notación de la derivada en el tiempo de una señal arbitraría y:
$$ \frac{\mathrm{d}y}{\mathrm{d}t}≡\dot{y}. $$
Esta es la denominada notación de Newton, o “flux notation” en inglés. Ahora, si sustituimos la aproximación de la derivada:
$$ \frac{y_k-y_{k-1}}{\Delta t}≈\dot y, $$
y resolvemos para el momento actual de la señal $y$:
$$ y_k \approx \dot y \Delta t + y_{k-1}, $$
¡Y esto es todo! Entonces, integrar una ecuación diferencial se convierte en un algoritmo de 3 pasos: Calcular la dinámica del sistema $\dot y$, multiplicar por el tiempo de muestreo $\Delta t$, y sumar el valor anterior de la señal y. Sencillo, ¿no?
Si se dieron cuenta, este algoritmo nos sirve para resolver derivadas de primer orden. En futuras entradas veremos como podemos generalizar el método para resolver un sistema dinámico de dimensión $n>1$. Esto nos permitirá estudiar sistemas más complejos, como por ejemplo un “Quadcopter”.
Acertijo: ¿Si, además de estudiar la velocidad del motor, también necesitamos estudiar la posición del motor. Qué necesitamos añadir a la simulación para que también calcule la posición del motor y no sólo la velocidad? Y la situación inversa también es válida: ¿Si necesitamos obtener la aceleración del motor a partir de la velocidad, ¿cómo sería el algoritmo en Python?
Insisto. Este tipo de problemas realmente se presentan en la industria. Recientemente, el equipo con el que trabajo necesitaba obtener la aceleración de un sistema mecánico, y el sistema sólo contaba con sensores de velocidad. ¿Qué harían en esta situación ustedes?
