
En entradas anteriores les platiqué cómo modelar un motor de corriente directa y cómo controlar la velocidad utilizando un controlador PID. En esta entrada les mostraré cómo diseñar un algoritmo de control de posición para el modelo de primer orden del motor de corriente directa. Es más, haremos algo que dejamos de lado en la entrada de control de velocidad: probaremos el controlador, diseñado a partir de un modelo de orden reducido, en el modelo de segundo orden del motor… y veremos qué pasa. A darle.
Recordemos que el modelo lineal, invariante, de un motor de corriente directa es:
$$ L\frac{di}{dt} + Ri +k_c\omega+ = v_{in}, \quad J\frac{d\omega}{dt}+k_f\omega=k_{\tau}i+\tau_l, $$
donde $L$ es la inductancia del motor, $R$ es la resistencia, $J$ es la inerncia del rotor, $k_f$ es el coeficiente de viscosidad, $k_c$ es la constante de fuerza contra-electromotriz, $v_{in}$ es el voltaje de alimentación del motor, o la señal de control. $k_\tau$ es la constante de torque del motor y $\tau_l$ es la carga del motor. $i$ es la corriente y $\omega$ es la velocidad del rotor.
Asumiendo que la inductancia del motor es mucho menor que la resistencia, es posible simplificar y obtener un modelo de orden reducido del motor:
$$ \frac{\Omega(s)}{V(s)}=\frac{K}{\tau s+1}, $$
donde:
$$ K=\frac{k_{\tau}}{Rk_f+k_{\tau}k_c}, \quad \tau=\frac{RJ}{Rk_f+k_{\tau}k_c}. $$
Si no te queda muy claro, no te preocupes, te invito a ver la entrada de modelado de un motor de corriente directa donde profundizamos más en la simplifcación que utilicé para llegar a estas ecuaciones.
Ahora, si prestas atención a la función de transferencia, está en función de la transformada de Laplace de la velocidad angular $\omega$ del motor. Para obtener la posición del motor a partir de una señal de velocidad es necesario integrar:
$$ \theta(t) = \int_{0}^t{\omega(\tau)\mathrm{d\tau}}. $$ La integral de una señal en el dominio de Laplace es equivalente a dividir por la variable de Laplace $s$, entonces es posible definir la posición en el dominio de Laplace:
$$ \Theta(s) = \frac{\Omega(s)}{s}. $$
Nótese que se asume que la velocidad inicial $\omega(0)=0$ para simplificar los cálculos al realizar la transformación de Laplace.
que se tiene la definición de la posición del rotor a partir de la velocidad, se realiza esta ecuación en el modelo de orden reducido del motor para obtener:
$$ \frac{\Theta(s)}{V(s)}=\frac{K}{s(\tau s+1)}. $$
Con este modelo de orden reducido del motor se realizará el análisis del sistema en lazo cerrado para calcular las ganancias del controlador.
Posicionamiento de Polos Comencemos el análisis insertando un controlador PID en el lazo de control. En el dominio de Laplace, un controlador PID se define de la siguiente forma:
$$ \frac{C(s)}{E(s)}=k_p+k_ds+\frac{k_i}{s}, $$
donde $k_i, k_d, k_p$ son las ganancias del controlador, y $E$ es el error del sistema: la diferencia entre la posición deseada $\theta_d$ y la posición real $\theta_r$ del motor, en este caso. Recuerda que la función de transferencia del sistema en lazo cerrado está dada por:
$$ \frac{Y(s)}{X(s)}=\frac{C(s)H(s)}{C(s)H(s)+1}, $$
donde $C(s)$ es la función de transferencia del controlador, y $H(s)$ es la función de transferencia del motor. $Y(s)$ es la salida del sistema, en este caso la velocidad del motor; y $X(s)$ es la entrada, en este caso el voltaje aplicado al motor. Si introducimos la función de transferencia del motor y el controlador en la ecuación del sistema en lazo cerrado, se tiene:
$$ \frac{\Omega(s)}{V(s)}=\frac{K(k_ds^2+k_ps+k_i)}{\tau{s}^3+(Kk_d+1)s^2+Kk_ps+Kk_i}. $$
Si recuerdas, la técnica de posicionamiento de polos consiste en seleccionar las ganancias del sistema para posicionar los polos dominantes del sistema en el lugar del plano complejo apropiado para lograr la respuesta deseada. Hay aspectos teóricos que se tienen que tener en cuenta a la hora de utilizar esta técnica, como la controlabilidad del sistema. Pero para no complicar demasiado esta introducción no profundizaré en esto, y si te interesa cononcer más sobre estos conceptos, te invito a consultar el libro “Modern Control Engineering”, de Katsuhiko Ogata.
Por el momento confía en mí: podemos posicionar los polos del sistema en cualquier lugar del plano complejo, como se verá más adelante. Si extraemos el polinomio característico del sistema, se tiene:
$$ \tau{s}^3+(Kk_d+1)s^2+ Kk_p{s}+Kk_i=0. $$
Si te das cuenta, la ganancia integral está aumentando el orden del sistema. Y tiene sentido, la dinámica del sistema ya tiene un integrador (velocidad a posición). Si eliminamos la ganancia integral, podemos reducir el orden del sistema, y el polinómio característico es ahora:
$$ {s}^2+\tau^{-1}(Kk_d+1)s+ \tau^{-1}Kk_p=0, $$
el cuál es de la forma:
$$ {s}^2+2\zeta\omega_n{s}+ {\omega_n}^2=0. $$
Entonces, por comparación podemos escoger las ganancias del sistema con la siguiente relación:
$$ k_d=\frac{2\zeta\omega_n{\tau}-1}{K},\quad k_p=\frac{\tau{\omega_n}^2}{K}, $$
donde $\omega_n$ es la frecuencia natural del sistema, y $\zeta$ es el factor de amortiguamiento.
Interesante, ¿no? Las ecuaciones para calcular las ganancias para un controlador de posición y de velocidad son idénticas; la diferencia es que para velocidad utilizamos un controlador PI, y para la posición utilizamos un controlador PD. Entonces podemos concluir que estas relaciones nos dan un punto de partida para escoger las ganancias de un controlador PID para motores de corriente directa. Y las ganancias están en función de los parámetros de desempeño deseado del sistema en lazo cerrado.
Simulación utilizando Python y Scipy En esta ocasión no utilizaremos el integrador sencillo que utilizamos en la entrada anterior. Utilizaremos la librería Scipy de cómputo científico escrita en Python que cuenta con métodos más sofisticados de integración numérica. La puedes encontrar aquí. Simularemos un motor de DC fabricado por Pittman. La hoja de especifícasiones la puedes encontrar por acá. Es un motor de tamaño considerable de 33 Watts o cerca de 0.4 HP, con un torque pico de 4.23 Nm. Los parámetros del motor son:
| Parámetro | Descripción | Valor |
|---|---|---|
| $R$ | Resistencia de armadura | $0.83\Omega$ |
| $J$ | Inercia del rotor | $2.37\mathrm{x}10^{-4}\mathrm{Kg-m^2}$ |
| $L$ | Inductancia de armadura | $2.31\mathrm{x}10^{-4}\mathrm{H}$ |
| $k_c$ | Constante de fuerza contra-electromotriz | $0.128\mathrm{V/rad/s}$ |
| $k_{\tau}$ | Constante de torque | $0.128\mathrm{Nm/A}$ |
| $k_f$ | Constante de fricción viscosa | $1.697\mathrm{x}10^{-3}\mathrm{Nm/rad/s}$ |
Si revisas la hoja de datos del motor te darás cuenta que no viene definido la constante de fricción viscosa $k_f$, sin embargo está definida en la tabla. Esto porque podemos calcularla a partir de los demás parámetros y las especificaciones de corriente nominal y velocidad nominal. Supongamos que el motor es energizado, incrementa su velocidad rápidamente hasta llegar al punto de operación estable sin carga, es decir, $\tau_l=0$. Bajo estas condiciones el rotor del motor ha dejado de acelerar: $\mathrm{d}\omega/\mathrm{d}t = 0$; todo el torque producido por el motor es consumido en equilibrar la fricción. Entonces, la segunda ecuación del modelo del motor se simplifica a:
$$ k_f\omega_{nom}=k_{\tau}{i_{nom}}. $$
Sustituyendo los valores de corriente y velocidad nominal del operación del motor, podemos concluir que la constante de fricción del motor es alrededor de $k_f=1.697×10^{-3}\mathrm{Nm/rad/s}$. Estos parámetros nos servirán para simular y verificar que el controlador, calculado con un modelo de orden reducido, funciona también para un modelo de segundo orden.
Primero veamos si el parámetro que acabamos de calcular es adecuado y la respuesta del motor es como se especifica en la hoja de datos. Para crear la simulación utilizaremos la función odeint del módulo integrate de scipy. La función tiene la interfaz odeint(dynamics, x0, t), donde el primer argumento de la función calcula la dinámica del sistema (en nuestro caso las ecuaciones dinámicas del motor), el segundo son las condiciones iniciales del sistema (velocidad y corriente inicial), y el tercer argumento es el vector de tiempo a través del cual se quiere simular el sistema. Esta función regresa la solución del sistema en espacio de estados evolucionando a través del tiempo.
La función que define la dinámica del sistema debe tener la interfaz apropiada para trabajar en conjunto con la función integrate. La interfaz es dynamics(x, t, *args), donde el primer argumento es el estado actual del sistema, que se utiliza para calcular la dinámica del sistema (recuerden las ecuaciones del motor, la derivada de la corriente y velocidad están en función de la corriente y la velocidad), el segundo argumento es el instante en el cual se está calculando la dinámica. El tercer argumento es opcional, lo utilizaremos para pasar las ganancias del controlador; ya verán más adelante. La función dynamics debe regresar un list o un numpy.array de dimensión (1, N), donde N es la dimensión del sistema (en nuestro caso, 2).
El código es el siguiente:
import numpy as np
import math
import matplotlib.pyplot as plt
import scipy.integrate
from scipy.integrate import odeint
class DCMotor(object):
def __init__(self, R = 1., L = 1., J = 1., kc = 1., kt = 1., kf = 1.,
x0 = None):
assert(R > 0. and L > 0. and J > 0. and kc > 0. and kt > 0. and kf > 0.)
self.params = {
'R': R, # Armature resistance.
'kf': kf, # Friction coefficient.
'kc': kc, # Back-emf constant.
'L': L, # Armature inductance.
'kt': kt, # Torque constant.
'J': J, # Rotor's moment of inertia.
}
self.A = np.array([[-kf / J, kt / J],
[-kc / L, -R / L]])
self.B = np.array([[0.],
[1. / L]])
def dynamics(self, x, t, *args):
try:
self.A.reshape(2, 2)
self.B.reshape(2, 1)
#self.x.reshape(3, 1)
dx = self.A.dot(x.reshape(2, 1)) + self.vin * self.B
except Exception:
raise ValueError('System dynamics dimension mismatch @ time {}'.format(t))
return dx.flatten()
if __name__ == '__main__':
motor = DCMotor(R = 0.83, L = 2.31e-3, J = 2.37e-4, kc = 0.128, kt = 0.128, kf = 0.001697)
t = np.arange(0, 0.1, 1e-3)
motor.vin = 90
y = odeint(motor.dynamics, [0., 0.], t)
for i, name in enumerate(['$\omega\,[\mathrm{rad/s}]$', '$i\,[\mathrm{amps}]$']):
plt.subplot(2, 1, i + 1)
plt.plot(t, y[:, i])
plt.ylabel(name)
plt.xlabel('$Time\,\mathrm{[s]}$')
plt.show()
El código está dividido en dos partes, prácticamente. En la parte superior se define la clase DCMotor que su única finalidad es aceptar los parámetros del motor, y calcular la dinámica del sistema en la función dynamics dado el estado actual y el voltaje de alimentación. Si se dan cuenta, la dinámica del motor está definida de una manera especial: con matrices. Esto solo tiene la finalidad de hacer más compactos u ordenados los cálculos. Esta manera de representar la dinámica de un sistema se denomina “Espacio de estados”, del inglés “State Space”. En espacio de estados la dinámica del motor se define de la siguiente forma:
Si llevas a cabo la multiplicación de matrices, deberás llegar al modelo que definimos al inicio de esta entrada. Nota que la función dynamics lleva a cabo precisamente esta multiplicación de matrices y regresa el valor calculado. ¡Y listo! scipy se encarga del resto.
En la segunda parte, el main, se ejecuta la simulación: se crea el motor a partir de los parámetros de la hoja de datos, se ejecuta la simulación por $100\mathrm{ms}$, con condiciones iniciales cero: $(\omega_0=0, i_0=0)$, con un voltaje constante de alimentación de $90\mathrm{v}$ (especificado en la hoja de datos), y se crea una gráfica con los resultados de la simulación:
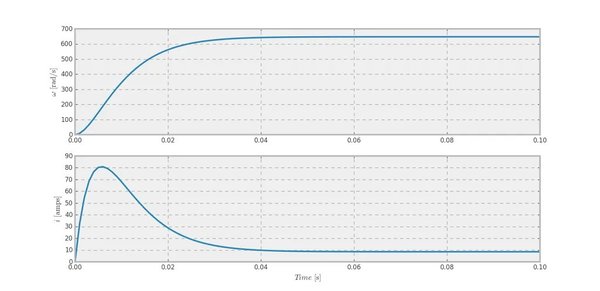 Figura 1. Respuesta a un escalón de $90\mathrm{v}$
Figura 1. Respuesta a un escalón de $90\mathrm{v}$
Veamos, la hoja de datos especifica que en condiciones de operación nominales del motor son: $(\omega_{nom}=6000\mathrm{RPM}\approx \ 628\mathrm{rad/s}, i_{nom}=8.33\mathrm{A})$. En la simulación obtuvimos: $(\omega_{nom}\approx 6178\mathrm{RPM}\approx \ 647\mathrm{rad/s}, i_{nom}\approx 8.6\mathrm{A})$. La corriente pico sí está bastante alejada de lo especificado en la hoja de datos; pero no hay manera de saber cuales fueron las condiciones de prueba. Tal vez la fuente de alimentación no tenía la potencia suficiente para lograr la corriente pico que vemos en la simulación. O tal vez la impedancia de salida de la fuente redujo la corriente pico que consume el motor.
Pero para las condiciones nominales de operación, estamos hablando de una discrepancia del $3$%. Lo cual, dependiendo de la aplicación y expectativa, podría ser suficiente, o no. También es posible comenzar el desarrollo con un modelo no tan preciso del sistema para hacer una validación rápida o prototipo, y a medida que el desarrollo avanza y se tiene más información sobre el sistema, el modelo es mejorado y se logra una mejor correlación entre el sistema real y el modelo. Para nuestros fines, podemos concluir que este modelo es suficiente. En entradas futuras podríamos ver cómo lograr un modelo más acertado incluyendo términos no lineales como la fricción seca, o variación de los parámetros del motor debido a las condiciones de operación.
Sigamos con el cálculo de las ganancias del sistema. Podrías hacerlo a lápiz y papel, pero si decides cambiar algún parámetro tendrías que hacerlo de nuevo. Mejor utilicemos la computadora, que para eso sirven. La función que calcula las ganancias es una mera implementación de las ecuaciones que obtuvimos en la sección de posicionamiento de polos. El código es el siguiente:
def compute_gains(Ts, Pos, R = 0., L = 0., J = 0., kc = 0., kt = 0., kf = 0.):
assert(Ts > 0. and Pos > 0. and R > 0. and L > 0. and J > 0. and kc > 0. and kt > 0. and kf > 0.)
motor_k = kt / (R * kf + kt * kc)
motor_t = R * J / (R * kf + kt * kc)
print('First order approximation parameters-> K: {}, Tau: {}'.format(motor_k, motor_t))
z = abs(math.log(Pos)) / math.sqrt((math.log(Pos)) ** 2 + math.pi ** 2)
wn = 4. / (z * Ts)
if -z * wn >= 0.:
print('Unstable system!!!')
print('System Response-> Natural freq: {}, Damping coefficient: {}'.format(wn, z))
print('Design parameters -> Max Overshoot: {}%, Settling time: {}s'.format(Pos * 100, Ts))
k1 = (2. * z * wn * motor_t - 1.) / motor_k # Zero-order coefficient.
k2 = (motor_t * wn ** 2) / motor_k # First-order coefficient.
print('Computed controller gains-> k1: {}, k2: {}'.format(k1, k2))
return k1, k2
La función recibe los parámetros del sistema, se asegura que todos sean estrictamente positivos (sería raro tener un motor con inercia negativa, ¿no?) e imprime mensajes útiles, como una advertencia si uno de los polos queda en el semiplano derecho. Al final regresa las ganancias del controlador. ¿Y por qué decidí nombrar las ganancias $k_1$, $k_2$ en lugar de $k_p$, $k_d$? Pues porque de esta forma podemos usar esta función para calcular las ganancias de un controlador de velocidad; recuerden que las ecuaciones son iguales.
Pero algo falta, ¿no? Estamos intentando diseñar el control de posición \theta del motor, ¡pero ninguna de las ecuaciones incluyen esta variable! Para solucionar esto aumentaremos el orden del sistema introduciendo la ecuación $\frac{\mathrm{d}\theta}{\mathrm{d}t}=\omega$ en el modelo en espacio de estados del sistema. Entonces el modelo aumentado sería:
Claro está que necesitamos aumentar el orden del sistema en la simulación también. Pero con esto ya podemos continuar con las simulaciones incluyendo la posición angular del rotor. La simulación estará escrita para durar $300\mathrm{ms}$, lo cual, para un controlador diseñado para lograr la posición en $100\mathrm{ms}$, es más que suficiente. La posición deseada será constante: con un valor de $7\mathrm{rad}$, aproximadamente una revolución del rotor. El código es el siguiente:
import numpy as np
import math
import matplotlib.pyplot as plt
import scipy.integrate
from scipy.integrate import odeint as ode
class DCMotor(object):
def __init__(self, R = 1., L = 1., J = 1., kc = 1., kt = 1., kf = 1.,
x0 = None):
assert(R > 0. and L > 0. and J > 0. and kc > 0. and kt > 0. and kf > 0.)
self.params = {
'R': R, # Armature resistance.
'kf': kf, # Friction coefficient.
'kc': kc, # Back-emf constant.
'L': L, # Armature inductance.
'kt': kt, # Torque constant.
'J': J, # Rotor's moment of inertia.
}
print('Motor parameters-> {}'.format(self.params))
self.vin = 0.
self.A = np.array([[0., 1., 0.],
[0., -kf / J, kt / J],
[0., -kc / L, -R / L]])
self.B = np.array([[0.],
[0.],
[1. / L]])
def dynamics(self, x, t, *args):
try:
self.A.reshape(3, 3)
self.B.reshape(3, 1)
dx = self.A.dot(x.reshape(3, 1)) + self.vin * self.B
except Exception:
raise ValueError('System dynamics dimension mismatch @ time {}'.format(t))
return dx.flatten()
def compute_gains(Ts, Pos, R = 0., L = 0., J = 0., kc = 0., kt = 0., kf = 0.):
assert(Ts > 0. and Pos > 0. and R > 0. and L > 0. and J > 0. and kc > 0. and kt > 0. and kf > 0.)
motor_k = kt / (R * kf + kt * kc)
motor_t = R * J / (R * kf + kt * kc)
print('First order approximation parameters-> K: {}, Tau: {}'.format(motor_k, motor_t))
z = abs(math.log(Pos)) / math.sqrt((math.log(Pos)) ** 2 + math.pi ** 2)
wn = 4. / (z * Ts)
if -z * wn >= 0.:
print('Unstable system!!!')
print('System Response-> Natural freq: {}, Damping coefficient: {}'.format(wn, z))
print('Design parameters -> Max Overshoot: {}%, Settling time: {}s'.format(Pos * 100, Ts))
k1 = (2. * z * wn * motor_t - 1.) / motor_k # Zero-order coefficient.
k2 = (motor_t * wn ** 2) / motor_k # First-order coefficient.
print('Computed controller gains-> k1: {}, k2: {}'.format(k1, k2))
return k1, k2
def simulation(x, t, *params):
motor, kp, kd, setpoint = params
motor.vin = kp * (setpoint - x[0]) + kd * (-x[1])
return motor.dynamics(x, t)
if __name__ == '__main__':
p_os, t_s = 0.05, 0.1 # Maximum overshoot and settling time.
tf, ts = 0.3, 1.0e-3
setpoint = 7.0 # Desired position.
x0 = [0.0, 0.0, 0.0] # Zero initial conditions.
m = DCMotor(R = 0.83, L = 2.31e-3, J = 2.37e-4, kc = 0.128, kt = 0.128, kf = 0.001697)
kd, kp = compute_gains(t_s, p_os, **m.params)
t = np.arange(0.0, tf + ts, ts)
y = ode(simulation, x0, t, args = (m, kp, kd, setpoint))
for i, name in enumerate(['$\\theta\,[\mathrm{rad}]$', '$\omega\,[\mathrm{rad/s}]$', '$i\,[\mathrm{amps}]$']):
ax = plt.subplot(3, 1, i + 1)
ax.plot(t, y[:, i], linewidth = 3.0)
ax.set_ylabel(name)
ax.set_xlim([t[0], t[-1]])
plt.xlabel('$Time\,\mathrm{[s]}$')
plt.show()
Lo primer diferencia es el modelo aumentado del motor para contener la posición angular del rotor. La función para calcular las ganancias es exactamente igual. Una segunda diferencia es que esta vez no se utiliza el método dynamics directamente para la función odeint. Se utiliza una función intermedia; la razón es que se necesita calcular el error y la señal de control antes de regresar la dinámica del motor. Pudimos haber incluído estos cálculos en la clase DCMotor, pero no tendría sentido mezclar la lógica de control con la dinámica del sistema. Nota que la función simulation calcula el error de la forma esperada: la diferencia entre la posición del motor, y la posición deseada; pero la parte derivativa está calculada de una manera distinta, ¿qué pasa aquí? Si se toma la derivada del error, se tiene:
$$ \frac{\mathrm{d}e}{\mathrm{d}t}=\frac{\mathrm{d}\theta_r}{\mathrm{d}t}-\frac{\mathrm{d}\theta}{\mathrm{d}t}. $$
¿Ahora ves? La derivada del error está definida como la diferencia entra la derivada de la posición deseada y la posición real del rotor. ¡Pero la posición deseada es constante! Entonces la derivada es cero, y la derivada del error es:
$$ \frac{\mathrm{d}e}{\mathrm{d}t}=-\omega. $$
Por que la ecuación para calcular el voltaje a partir del controlador PD es:
$$ u=k_p(\theta_d-\theta)-k_d\omega; $$
y listo, este es el control de posición del motor. Se aplica el voltaje, se calcula la dinámica del sistema a partir del nuevo voltaje aplicado y se integra durante el tiempo determinado. Al terminar la simulación, se grafican los resultados. Si todo va bien, deberías ver una gráfica como la siguiente:
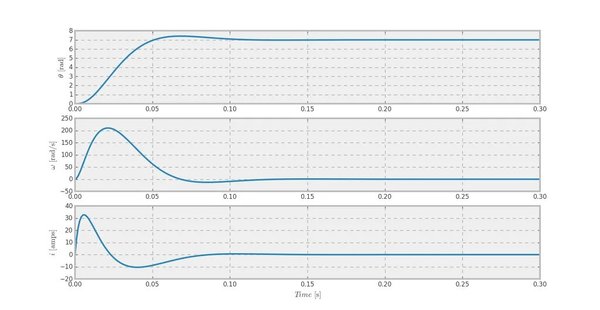 Figura 2. Respuesta del modelo del motor Pittman en lazo cerrado
Figura 2. Respuesta del modelo del motor Pittman en lazo cerrado
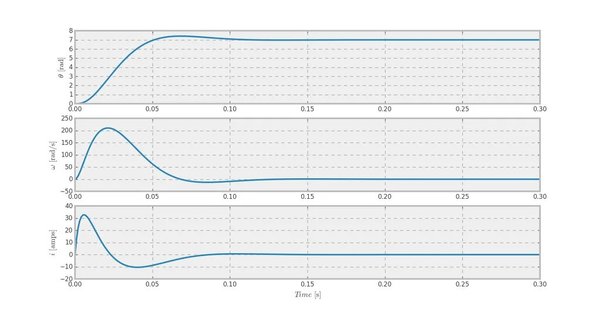 Figura 3. Respuesta del modelo del motor Pittman con control de posición
Figura 3. Respuesta del modelo del motor Pittman con control de posición
Puedes darte cuenta que el sistema tiene el desempeño deseado: el sobretiro se encuentra cercano al valor deseado, y de manera similar el tiempo de asentamiento. Aún cuando el control de posición fue diseñado utilizando un modelo reducido del motor, funciona para el sistema de segundo orden. Esto se debe a que $L << R$. Y para demostrar esto, intenta incrementar el valor de L diez veces. Deberías ver algo similar a la siguiente imagen:
Respuesta del control de posición del modelo con $L=2.31×10^{-2}$. Y esto debido a que el modelo ya no se puede aproximar como un sistema de primer orden. En la práctica, la inductancia del devanado de los motores es mucho menor que la resistencia de este. Esto es inherente a la construcción de los motores, debido a esto tienen respuestas al escalón aproximables como sistemas de primer oden.
Discusión
¿Pero, cuánto voltaje se necesita para lograr esta respuesta? Queda claro cuanta corriente, pues es parte de los estados del sistema y la función de integración calcula estos valores. ¿Cómo podemos hacer para graficar también el voltaje? La solución sencilla es simplemente agregarlos a una lista y graficarla al final. Pero esta no es una solución elegante, existen mejores maneras de hacer esto.
Además, tuvimos “suerte” en poder calcular la derivada del error utilizando la velocidad del rotor ya que la posición deseada era constante. ¿Qué sucede si la posición deseada es una trayectoria que varía en el tiempo? En este caso tenemos que implementar algún tipo de algoritmo para derivar el error de forma numérica. Ahora, hemos controlado la posición y velocidad del sistema; pero supongamos que la aplicación necesita controlar el torque del motor. ¿Cómo podemos diseñar un controlador para controlar el torque del motor? ¿Qué sucedería si unimos el controlador de torque, velocidad y posición para formar un controlador en cascada? ¿Cuál sería la diferencia en desempeño?
En futuras entradas responderemos estas preguntas.
